Taking Logarithms of Growth Rates and Log-based Data.

A usual practice while we’re handling economic data, is the use of logarithms, the main idea behind using them is to reduce the Heteroscedasticity -HT- of the data (Nau, 2019). Thus reducing HT, implies reducing the variance of the data. Several times, different authors implement some kind of double logarithm transformation, which is defined as taking logarithms of the data which is already in logarithms and growth rates (via differencing logarithms).

The objective of this article is to present the implications of this procedures, first by analyzing what does do the logarithm to a variable, then observing what possible inferences can be done when logarithms are applied to growth rates.

There are a series of properties about the logarithms that should be considered first, we’re not reviewing them here, however the reader can check them in the following the citation (Monterey Institute, s.f). Now let’s consider a bivariate equation:

The coefficient B represents the marginal effect of a change of one unit in X over Y. So, interpreting the estimation with ordinary least squares estimator gives the following analysis: When x increases in one unit, the result is an increase of B in y. It’s a lineal equation where the marginal effect is given by:

When we introduce logarithms to the equation of (1) by modifying the functional form, the estimation turns to be non-linear. However, let’s first review what logarithms might do to the x variable. Suppose x is a time variable which follows an upward tendency, highly heteroscedastic as the next graph shows.

We can graphically appreciate that variable x has a positive trend, and also that has deviations over his mean over time. A way to reduce the HT present in the series is to make a logarithm transformation. Using natural logarithms, the behavior is shown in the next graph.

The units have changed drastically, and we can define that logarithm of x is around 2 and 5. Whereas before we had it from 10 to 120 (the range has been reduced). The reason, the natural logarithm reduces HT because the logarithms are defined as a monotonic transformation (Sikstar, s.f.). When we use this kind of transformation in econometrics like the following regression equation:

The coefficient B is no longer the marginal effect, to interpret it we need to divide it by 100 (Rodríguez Revilla, 2014). Therefore, the result should be read as: an increase of one unit in x produces a change of B/100 in y.

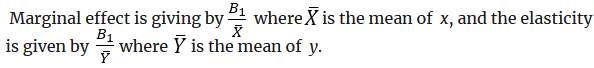
If we use a double-log model, equation can be written as:

In this case, the elasticity is simply B which is interpreted in percentage. Example, if B=0.8. By an increase of 1% in x, the result would be an increase of 0.8% in y.

On the other hand, if we use log-linear model, equation can be written as:

In this case, B must be multiplied by 100 and it can be interpreted as a growth rate in average per increases of a unit of x. If x=t meaning years, then B is the average growth per year of y.

The logarithms also are used to calculate growth rates. Since we can say that:

The meaning of equation (5) is that growth rates of a variable (left hand of the equation) are approximately equal to the difference of logarithms. Returning with this idea over our x variable in the last graphic, we can see that the growth rate between both calculations are similars.

It’s appreciably the influence of the monotonic transformation; the growth rate formula has more upper (positive) spikes than the difference of logarithms does. And inversely the lower spikes are from the difference of logarithms.  Yet, both are approximately growth rates which indicate the change over time of our x variable.

For example, let’s place on the above graphic when is the 10^th year.  The difference in logarithms indicates that the growth rate is -0.38% while the growth rate formula indicates a -0.41% of the growth-related between year 9^th and now.  Approximately it’s 0.4% of negative growth between these years.

When we use logarithms in those kinds of transformations we’ll get mathematically speaking, something like this:

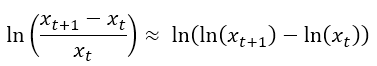
Some authors just do it freely to normalize the data (in other words reducing the HT), but Would be the interpretation remain the same? What are the consequences of doing this? It’s something good or bad?

As a usual answer, it depends. What would happen if, for example, we consider the years 9 and 10 again of our original x variable, we can appreciate that the change it’s negative thus the growth rate it’s negative. Usually, we cannot estimate a logarithm when the value is negative.

With this exercise, we can see that the first consequence of overusing logarithms (in differenced logarithms and general growth rates) is that if we got negative values, the calculus becomes undefined, so missing data will appear. If we graph the results of such thing, we’ll have something like this:

At this point, the graphic takes the undefined values (result of the logarithm of negative values) as 0 in the case of Excel, other software might not even place a point.  We got negative values of a growth rate (as expected), but what we got now is a meaningless set of data. And this is bad because we’re deleting valuable information from other timepoints.

Let’s forget for now the x variable we’ve been working with.  And now let’s assume we got a square function.

The logarithm of this variable since its exponential would be:

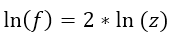
and if we apply another log transformation, then we’ll have:

However, consider that if z=0, the first log would be undefined, and thus, we cannot calculate the second. We can appreciate this in some calculations as the following table shows.

The logarithm of 0 is undefined, the double logarithm of that would be undefined too. When z=1 the natural logarithm is 0, and the second transformation is also undefined. Here we can detect another problem when some authors, in order to normalize the data, apply logarithms indiscriminately. The result would be potential missing data problem due to the monotonic transformation when values of the data are zero.

Finally, if we got a range of data between 0 and 1, the logarithm transformation will induce the calculus to a negative value. Therefore, the second logarithm transformation it’s pointless since all the data in this range is now undefined.

The conclusions of this article are that when we use logarithms in growth rates, one thing surely can happen: 1) If we got potential negative values in the original growth rate, and then apply logarithms on those, the value becomes undefined, thus missing data that will occur. And the interpretation becomes harder. Now if we apply some double transformation of log values, the zero and the negative values in the data will become undefined, thus missing data problem will appear again. Econometricians should take this in considerations since it’s often a question that arises during researches, and in order to do right inferences, analyzing the original data before applying logarithms should be a step before doing any econometric procedure.

Bibliography

Monterey Institute. (s.f). Properties of Logarithmic Functions. Obtained from: http://www.montereyinstitute.org/courses/DevelopmentalMath/TEXTGROUP-1-19_RESOURCE/U18_L2_T2_text_final.html

Nau, R. (2019). The logarithm transformation. Obtenido de Data concepts The logarithm transformation. Obtained from: https://people.duke.edu/~rnau/411log.htm

Rodríguez Revilla, R. (2014). Econometria I y II. Bogotá. : Universidad Los Libertadores.

Sikstar, J. (s.f.). Monotonically Increasing and Decreasing Functions: an Algebraic Approach. Obtained from: https://opencurriculum.org/5512/monotonically-increasing-and-decreasing-functions-an-algebraic-approach/