Econometrics

Performing a parallel pre-trend test in universal absorbing treatments in R

Leave a Comment / Econometrics /

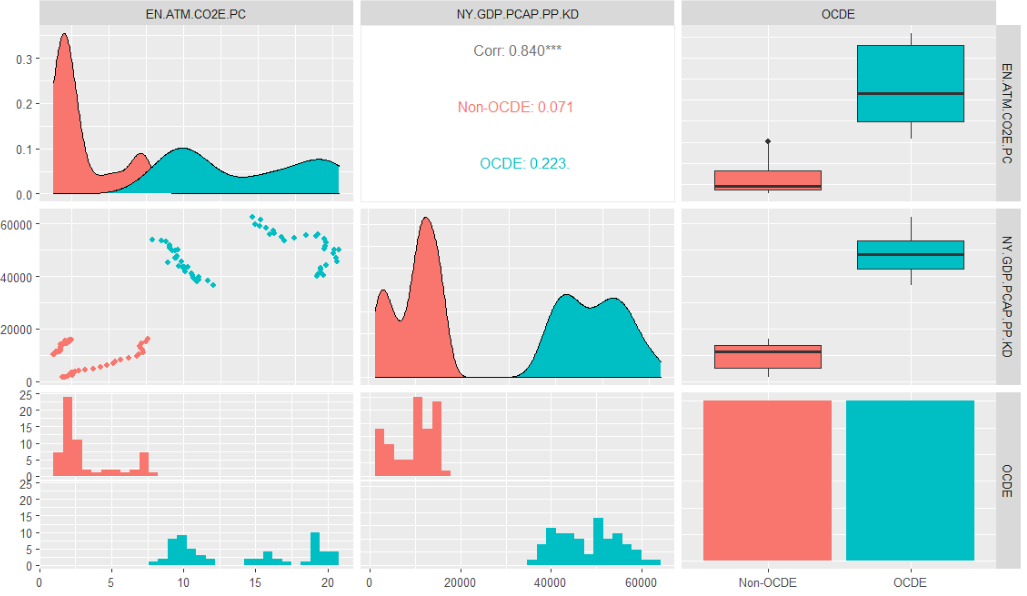
Introduction In a recent paper from the Journal of Research, Innovation and Technologies published last year, there was a significant discussion (Riveros Gavilanes, 2023) about how control variables might be related to the fulfillment of parallel trends in event study (or dynamic differences-in-differences) of panel data. In this article, we will replicate such paper and […]

Performing a parallel pre-trend test in universal absorbing treatments in R Read More »

How to learn Macroeconomic CGE Modeling?

Leave a Comment / Econometrics, General economics, Researching /

What is CGE Modeling? Computable General Equilibrium (CGE) modeling is a type of economic modeling used to study the impacts of economic policies and shocks on the economy as a whole. The goal of CGE modeling is to provide a comprehensive and consistent representation of the interactions among different sectors and agents within an economy.

How to learn Macroeconomic CGE Modeling? Read More »

Endogenous co-regressor… Not what you think!

Leave a Comment / Econometrics /

In classic econometrics textbooks and classes, we often associate endogeneity to the correlation or relationship with the error term from a regressor. This is correct and fully agreed upon across authors and professors. But there’s some kind of new endogenous behavior that may not be correlated with the error/residual only, and it may be a

Endogenous co-regressor… Not what you think! Read More »

Modeling Asset Prices with Geometric Brownian Motion in Python

3 Comments / Econometrics, General economics /

One landmark theorem in Financial Economics is the Efficient Market Hypothesis (EMH). This theorem posits that in an arbitrage-free market, we can model an asset’s present price as the discounted expected future price: We can take the natural logarithm to show that the natural logarithm of asset prices follows a random walk – the best

Modeling Asset Prices with Geometric Brownian Motion in Python Read More »

Threat to validity of regression analysis – Omitted Variables Bias

Leave a Comment / Econometrics, General economics /

Most of the readers of this blog would be familiar with ordinary least squares estimator and regression models. Let us talk about one source that can cause these estimates and models to be biased and inconsistent. This is especially important when we think about the causal relationship of interest or the relationship which being studied.

Threat to validity of regression analysis – Omitted Variables Bias Read More »