In the last month, while I was researching through the literature of the military expenditure and economic growth, I found a little statement from an article, which appointed one of the things less discussed in econometrics, such statement is:
“The Holy Grail of applied econometrics is a tight theoretical model, which fits the data well. Like the Holy Grail, such models are hard to find.” (Dunne, Smith, & Willenbockel, 2005)
When one, as a researcher meditate this, one really knows that matching theoretical models with regression equations it’s indeed hard. Even when econometrics can be defined as the measure and validation part of the economic science, the relationships which are addressed to study are not exactly as accurate as the theory states.
I want to put an example, let’s see the conclusions of the Solow Swan (1956) model with technology. which are compiled in the next equation.
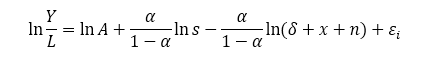
Where Y/L is the gross domestic product -GDP- of the economy measured in per capita units, A is a level of technology, α is the elasticity of the aggregate stock of capital of the economy, s is an exogenous saving rate, δ is the depreciation rate, x is the growth rate of the technology, and n is the growth rate of the population.
The term ε is just added as the stochastic error in the equation to proceed with the regression analysis, which theoretically is defined as independent of the variables in the regression and represents external shocks in the per capita product. However, if this doesn’t happen in the time series context, it could be possible that this term contains all the variables not included in the regression, therefore violating the exogeneity assumption and inducing an omitted variable bias with misspecification.
Basically, the model is telling us that the growth of the economy is positively given by the technology and the rate of saving of the economy which is invested in physical capital.
Now the Augmented Solow-Model proposed by Mankiw, Romer & Weil (1992) also known as the MRW model, concludes the following:
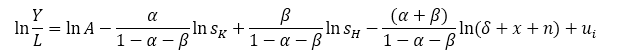
Where we got some new terms denoted with β as the elasticity of the aggregate stock of human capital in the production function, and separated terms of the savings, denoted by s_k as the saving rate dedicated to the accumulation of physical capital and s_h which is the saving rate dedicated to the accumulation of human capital.
The Augmented Model proposed by Mankiw, Romer & Weil has more variables in the specification of the growth of the economy.
Which one is correct? The answer relies on the regressions they have performed with both models, in general, the augmented model explains better the economic growth and the convergence of the economies than the simple Solow-Swan model.
The simple Solow-Swan model has a problem in the specification and an omitted variable problem, the augmented Solow-Swan model correct this by introducing the measure and importance of human capital accumulation. Both are theoretical constructions, but the augmented model fits better in reality than the original model.
Going further, one could ask if it would be wrong to consider all variables as endogenous? In the last two models, we have seen that the savings of physical or human capital are exogenous along with the growth rate of technology, but more theoretical considerations, like the Ramsey (1928) model could determinate the savings as endogenous, even the depreciation and the technology can be endogenized, so regressing the above equation with two-stage or three-stage least squares would be the best approach.
Considering this set of ideas, econometricians then will have to face a difficult situation when the theoretical approach might not be suitable for the reality of the sample, and I say this because this is a complex world, where a single explanation for all the situations is not plausible.
We need to remember also, that the whole objective of the theory is to explain reality, and if this theory fails to succeed in this objective, even the most logical explanation would be useless. Something completely out of sense is to modify reality to match with the theory.
The holy grail then would be the adequacy of the theory with the reality, and in econometrics, this means that we need to find a strong theoretical framework that matches our data generating process. But the validation techniques should have some logical approaches considering the assumptions of the regression.
Going backward, before theory and empirical methods, we are interested in finding the truth, and this truth goes from discovery existing or non-existing relationships and causality, in order to explain reality. Such findings, even when they start from a deviated or wrong approach are useful to build the knowledge.
A great example of this is the Phillip’s Curve (Phillips, 1958), it started as an empirical fact which correlated positive rates of inflation with employment, and then it began to be strongly study on Phelps (1967) and Friedman (1977) with more theoretical concepts as rational expectations over the phenomenon of inflation.
Econometricians should then do research with logical economic sense when they are heading to estimate relationships, but have to be aware that samples and individuals are not the same in the space (they change according to locations and the time itself). However, the theoretical framework is the main basis we need to always consider during the economic research, but also remember we can propose a new theoretical framework, to explain the reality on the basis of facts and past theories.
Bibliography
Dunne, J., Smith, R. P., & Willenbockel, D. (2005). MODELS OF MILITARY EXPENDITURE AND GROWTH: A CRITICAL REVIEW. Defence and Peace Economics, Volume 16, 2005 – Issue 6, 449-461.
Friedman. (1977). Nobel Lecture Inflation and Unemployment. Journal of Political Economy, Vol. 85, No. 3 (Jun., 1977), 451-472.
Kwat, N. (2018). The Circular Flow of Economic Activity. Obtenido de Economics Discussion: http://www.economicsdiscussion.net/circular-flow/the-circular-flow-of-economic-activity/18159
Mankiw, N. G., Romer, D., & Weil, N. D. (1992). A CONTRIBUTION TO THE EMPIRICS OF ECONOMIC GROWTH. Quarterly Journal of Economics, 407- 440.
Marmolejo, I. (2012). Indifference Curve Confusion and Possible Critique. Obtenido de Radical Subjectivist: https://radicalsubjectivist.wordpress.com/2012/02/10/indifference-curve-confusion-and-possible-critique/
Nicholson, W. (2002). Microeconomic Theory. México D.F.: Thompson Learning.
Phelps, E. (1967). Phillips Curves, Expectations of Inflation and Optimal Unemployment over Time . Economica, New Series, Vol. 34, No. 135 (Aug., 1967), 254-281.
Phillips, A. W. (1958). The Relation between Unemployment and the Rate of Change of Money Wage Rates in the United Kingdom, 1861-1957. Economica, New Series, Vol. 25, No. 100. (Nov., 1958),, 283-299.
Ramsey, F. P. (1928). A mathematical theory of saving. Economic Journal, vol. 38, no. 152,, 543–559.
Solow, R. (1956). A Contribution to the Theory of Economic Growth. The Quarterly Journal of Economics, Vol. 70, No. 1 (Feb., 1956),, 65-94.

Woah! I’m really enjoying the template/theme of this website.
It’s simple, yet effective. A lot of times it’s very hard to get that “perfect balance” between usability and
visual appeal. I must say you have done a very good job with this.
Also, the blog loads super fast for me on Internet explorer.
Excellent Blog!