Box-Pierce Test of autocorrelation in Panel Data using Stata.

The test of Box & Pierce was derived from the article “Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models” in the Journal of the American Statistical Association (Box & Pierce, 1970).

The approach is used to test first-order serial correlation, the general form of the test is given the statistic as:

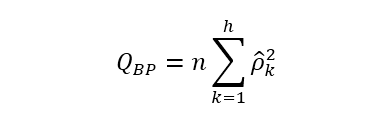
Where the statistic of Box- Pierce Q is defined as the product between the number of observations and the sum of the square autocorrelation ρ in the sample at lag h. The test is closely related to the Ljung & Box (1978) autocorrelation test, and it used to determine the existence of serial correlation in the time series analysis. The test works with chi-square distribution by the way.

The null hypothesis of this test can be defined as H0: Data is distributed independently, against the alternative hypothesis of H1: Data is not distributed independently. Therefore, the null hypothesis is that data is not suffering from an autocorrelation structure against the alternative which proposes that the data has an autocorrelation structure.

The test was implemented in Stata with the panel data structure by Emad Abd Elmessih Shehata & Sahra Khaleel A. Mickaiel (2004), the test works in the context of ordinary least squares panel data regression (the pooled OLS model). And we will develop an example here.

First we install the package using the command ssc install as follows:

ssc install lmabpxt, replace

Then we will type help options.

help lmabpxt

From that we got the next result displayed.

We can notice that the sintax of the general form is:

lmabpxt depvar indepvars [if] [in] [weight] , id(var) it(var) [noconstant coll ]

In this case id(var) and it(var) represents the identificatory of individuals (id) and identificatory of the time structure (it), so we need to place them in the model.

Consider the next example

clear all
use http://www.stata-press.com/data/r9/airacc.dta
xtset airline time,y
reg pmiles inprog
lmabpxt  pmiles inprog, id(airline) it(time)

Notice that the Box-Pierce test implemented by Emad Abd Elmessih Shehata & Sahra Khaleel A. Mickaiel (2004) will re-estimate the pooled regression. And the general output would display this:

In this case, we can see a p-value associated to the Lagrange multiplier test of the box-pierce test, and such p-value is around 0.96, therefore, with a 5% level of significance, we cannot reject the null hypothesis, which is the No AR(1) panel autocorrelation in the residuals.

Consider now, that you might be using fixed effects approach. A numerical approach would be to include dummy variables (in the context of least squares dummy variables) of the individuals (airlines in this case) and then compare the results.

To do that we can use:

tab airlines, gen(a)

and then include from a2 to a20 in the regression structure, with the following code:

lmabpxt  pmiles inprog a2 a3 a4 a5 a6 a7 a8 a9 a10 a11 a12 a13 a14 a15 a16 a17 a18 a19 a20 , id(airline) it(time)

This would be different from the error component structure, and it would be just a fixed effects approach using least squares dummy variable regression. Notice the output.

Using the fixed effects approach with dummy variables, the p-value has decreased significantly, in this case, we reject the null hypothesis at a 5% level of significance, meaning that we might have a problem of first-order serial correlation in the panel data.

With this example, we have done the Box-Price test for panel data (and additionally, we established that it’s sensitive to the fixed effects in the regression structure).

Notes:

The lmabpxt appears to be somewhat sensitive if the number of observations is too large (bigger than 5000 units).

There are an incredible compilation and contributions made by Shehata, Emad Abd Elmessih & Sahra Khaleel A. Mickaiel which can be found in the next link:

http://www.haghish.com/statistics/stata-blog/stata-programming/ssc_stata_package_list.php

I suggest you to check it out if you need anything related to Stata.

Bibliography

Box, G. E. P. and Pierce, D. A. (1970) “Distribution of Residual Autocorrelations in Autoregressive-Integrated Moving Average Time Series Models”, Journal of the American Statistical Association, 65: 1509–1526. JSTOR 2284333

G. M. Ljung; G. E. P. Box (1978). “On a Measure of a Lack of Fit in Time Series Models”. Biometrika 65 (2): 297-303. doi:10.1093/biomet/65.2.297.

Shehata, Emad Abd Elmessih & Sahra Khaleel A. Mickaiel (2014) LMABPXT: “Stata Module to Compute Panel Data Autocorrelation Box-Pierce Test”